Performance Graphs Are Back

My old website had them and some people have asked about them and now they are back. I have stability and drag (how much force is needed to go a given speed) data for most of my designs.

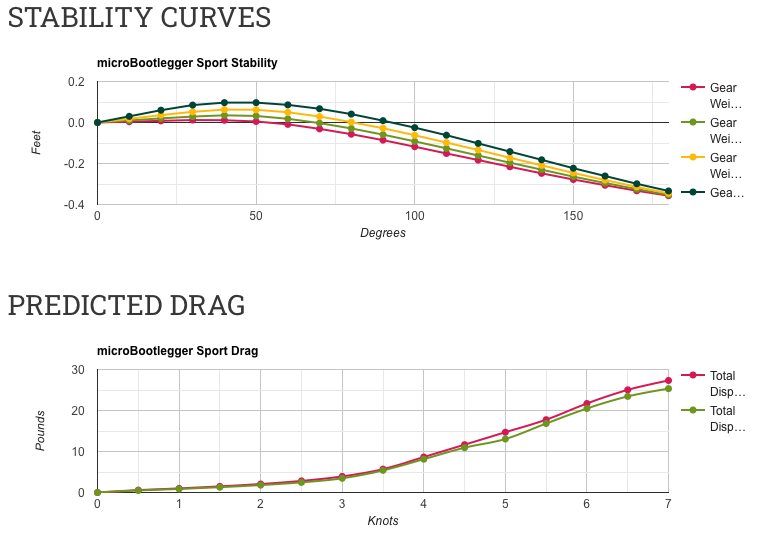
Stability:

These graphs show how much torque it takes to hold the kayak at a given angle of lean. On the left (0°) is upright and on the left is completely upside down (180°).

The stability is modeled with several different paddler weights and several different weights for gear. The paddler (or rower) is assumed to be seated in the kayak with their center of gravity 10-inches above the seat, directly with the boat center of buoyancy and the gear is centered in the volume of the boat. The weight of the boat is also factored into the calculation. The paddler is assumed to be sitting bolt upright in the seat and does not do anything to correct for the boat leaning.

What is being graphed is actually the side-to-side horizontal distance between the center of gravity of the paddler/gear/boat system and the center of buoyancy at various angles between 0° and 180°. This sometimes called G_Z. What this tells us is how long the lever arm is that is forcing the boat to tip. When the numbers are positive, that means the boat wants to turn back upright, i.e. it is "stable". The moment trying to force the boat back upright is the combined weight of the boat and everything in it times the distance G_Z giving you foot-pounds of torque. When the number goes negative, that means the weight of the paddler/gear/boat system is out beyond the center of buoyancy and the torque is actually trying to dump you in the water.

I generally have modeled the stability with two different weight paddlers and each with or without gear in the boat. Heavier paddlers tend to make the boat less stable because their weight raises the center of gravity. Heavier gear tends to make the boat more stable as the weight lowers the center of gravity.

Initial Stability

Kind of like it says, "Initial" stability is how stable the boat feels when it is floating upright normally. Some boats will feel very solid when you sit in them, other will be a bit twitchy - feeling like they don't want to settle down. To get an idea about initial stability, look at the first part of the graph all the way over on the left. Look at how quickly the lines rise up from the zero point (zero degrees is floating upright with no lean). Those boats where the curve rises quickly will feel more stable. Boats where the curve is almost flat and rises very little or slightly will tend to feel unstable. 

Secondary Stability

There are some boats that feel really unstably at first, but if are hard to capsize. If you lean hard out to one side, they find a spot where it is hard to tip them over more. This is secondary stability. Secondary stability is often characterized by how high the top of the stability curve gets. This is the maximum torque you can put on the boat without it capsizing. As you lean farther at requires less and less effort to make the boat tip farther and farther.

Ultimate Stability

It may seem like this is the most important but really it is initial and secondary stability that most effect how comfortable we are in a boat. Ultimate stability is how much work it takes to finally get the boat to the point of no-return. When the curve crosses the zero line and becomes negative, the boat would now rather go completely upside down than return to upright. Technically, this is the area under the curve for the positive parts of the stability curve. Look for boats with a high maximum G_Z combined with zero-crossing as far to the right as possible. Boats with higher curves will be harder to tip, and boats with longer positive stability can be tipped at a more severe angle and still return upright.

Drag:

The drag graphs are based on the modeling system created by John Winters for the old Sea Kayaker Magazine for their kayak evaluations and reviews. As of this writing you could still find the Excel modeling spread sheet on the Mariner Kayaks website. These models are based on some testing Sea Kayaker had done on sea kayaks and then refined by John. I am using a version of the Excel spread sheet.

In this case "drag" is the predicted force that is required to make the boat move a certain speed through the water. Boats with lower drag at a certain speed are easier to move at that speed, and conversely if you are able to make your paddle or oars produce a certain amount of force, the boat with lower drag will go faster when you are paddling that hard.

Drag is a function of primary sources. Friction from water sliding along the underwater surface of the boat is the primary source of drag at low speeds. As speed increases, the wake created by the boat pushing water out of the way becomes more important. Moving that water out and back around the shape/form of the boat requires energy, and the faster it moves the more energy required. At the top end speed, the form drag dominates over the frictional drag.

Generally, boats with lower wetted surface areas will have less frictional drag, and longer boats will have less form drag. As a result short boats are often easier to paddle (faster) at low speeds, and long boats are faster at high speeds.

Like the stability curves, I have generally modeled the drag with a couple scenarios: with the boat carrying just the paddler/rower and with the paddler plus some gear. Typically, more total weight will require more power to move around, so the drag will be higher.

Reading the Graphs

At the time I am writing this blog post, I am still trying to improve the display of the data. The legends are hard to read, but if you over your mouse over the dots on the curves, you will see more information about each curve.

It is my goal to have these graphs plotted on the comparison page as well, but that part of the project is not yet completed.